Tam giác là gì?
Hình tam giác là hình phẳng được tạo ra bởi 3 điểm không thẳng hàng được gọi là 3 đỉnh của tam giác. Ba đoạn thẳng nối các đỉnh này được gọi là 3 cạnh của tam giác. Tổng 3 góc của tam giác luôn bằng 180 độ. Hình tam giác là hình có số cạnh ít nhất trong hình học phẳng.
Phân biệt các loại tam giác
Có thể phân loại tam giác theo các tiêu chí:
* Theo độ dài cạnh:
| Tên loại tam giác | Đặc điểm | Hình minh họa |
|---|---|---|
| Tam giác thường | Tam giác thường có ba cạnh có độ dài khác nhau, số đo 3 góc khác nhau |
 |
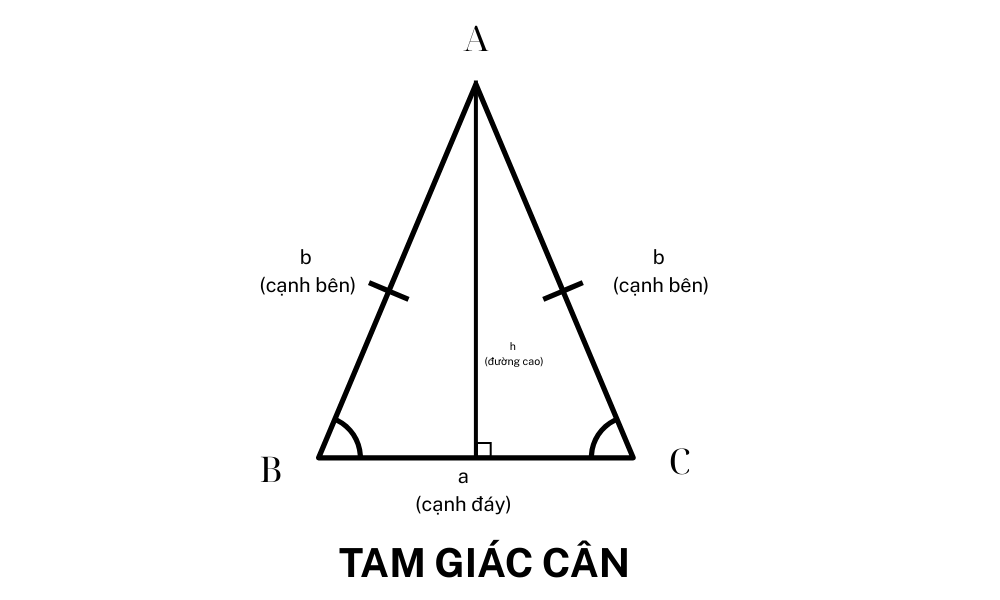
| Tam giác cân | Tam giác cân có ít nhất 2 cạnh bằng nhau gọi là 2 cạnh bên, 2 góc ở đáy tương ứng với 2 cạnh bên này cũng bằng nhau |
 |
* Theo số đo góc:
| Tên loại tam giác | Đặc điểm | Hình minh họa |
|---|---|---|
| Tam giác vuông | Tam giác vuông có 1 góc vuông (bằng 90 độ). Cạnh đối diện với góc vuông là cạnh huyền, hai cạnh còn lại là cạnh góc vuông. |
 |
| Tam giác nhọn | Tam giác nhọn có cả 3 góc đều nhỏ hơn 90 độ (đều là góc nhọn) |
 |
| Tam giác tù | Tam giác tù có 1 góc lớn hơn 90 độ (gọi là góc tù) |
 |
* Trường hợp đặc biệt kết hợp 2 tiêu chí độ dài cạnh và số đo góc:
| Tên loại tam giác | Đặc điểm | Hình minh họa |
|---|---|---|
| Tam giác vuông cân | Tam giác vừa là tam giác vuông, vừa là tam giác cân |
 |
| Tam giác đều | Tam giác có 3 cạnh bằng nhau và 3 góc đều bằng 60 độ |
 |
Công thức tính diện tích tam giác
Công thức tính diện tích có thể áp dụng chung cho toàn bộ các loại tam giác thường là tích của chiều cao của tam giác với độ dài cạnh đáy rồi chia 2.
| S = (a x h)/2 |
Trong đó:
S: Diện tích tam giác
a: Độ dài cạnh đáy
h: Chiều cao của tam giác, là đoạn thẳng kẻ từ đỉnh vuông góc xuống cạnh đáy a
 |
 |
 |
Ví dụ: Tính diện tích tam giác ABC có độ dài đáy là 4cm, chiều cao là 3cm.
Đáp số: Diện tích tam giác ABC là: S = (4 x 3)/2 = 6 (cm2)
Công thức tính diện tích tam giác vuông
Công thức tính diện tích tam giác vuông bằng tích 2 cạnh góc vuông rồi chia 2
| S = (a x b)/2 |
Trong đó:
S: Diện tích tam giác
a, b: Độ dài 2 cạnh góc vuông bởi a tương ứng với chiều cao còn b tương ứng với đáy của tam giác.

Ví dụ: Tính diện tích tam giác ABC vuông ở góc B có các cạnh AB = 5cm, BC = 3cm, AC = 6cm.
Đáp số: Diện tích tam giác ABC là: S = (5 x 3)/ 2 = 7,5 (cm2)
Công thức tính diện tích tam giác vuông cân
Công thức tính diện tích tam giác vừa vuông vừa cân bằng bình phương 2 cạnh góc vuông rồi chia 2.
| S = (a2) / 2 |
Trong đó:
S: Diện tích tam giác
a: Độ dài cạnh góc vuông.

Ví dụ: Tính diện tích tam giác ABC vuông cân ở góc B có các cạnh AB = BC = 6cm, AC = 7cm.
Đáp số: Diện tích tam giác ABC là: S = (62)/ 2 = 18 (cm2)
Cách tính diện tích tam giác khi biết độ dài 3 cạnh
Áp dụng công thức Heron, khi biết độ dài 3 cạnh của tam giác lần lượt là a, b, c.
Đầu tiên tính nửa chu vi tam giác: p = (a + b + c) / 2
Tiếp theo tính diện tích tam giác: S = √[p x (p - a) x (p - b) x (p - c)]
Cách tính diện tích tam giác khi biết 2 cạnh và góc xen giữa
Nếu biết độ dài hai cạnh và góc xen giữa của tam giác, ta có công thức:
S = (1/2) x a x b x sin(C) (với a, b là độ dài hai cạnh, C là góc xen giữa)
Những lưu ý khi tính diện tích tam giác
Cần xác định rõ loại hình tam giác để áp dụng cách tính diện tích phù hợp.
Các độ dài cạnh, chiều cao phải quy về chung một hệ đơn vị độ dài
Kết quả về diện tích phải tính bằng đơn vị vuông (cm2, m2…)


